| 1: | = | ||
| Rise:Run | Degrees |
What angles do 1:6, 1:7, 1:8 correspond to?
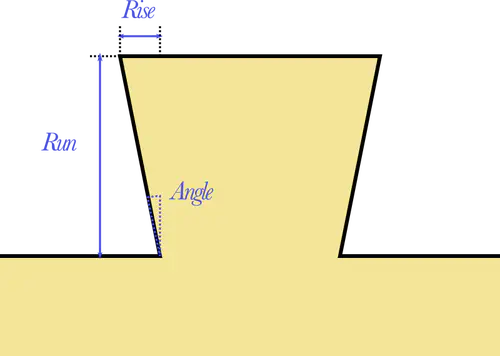
Dovetails angles are often specified as a Rise:Run ratio, for example 1:7. This corresponds to the angle of a line that covers a vertical distance of 7 cm (or inches, or whatever unit you prefer) and deflects horizontally by 1 cm (or inches, or whatever unit you prefer).
Here are the angles that these rise:run ratios correspond to:
| Rise:Run | Angle |
|---|---|
| 1:1 | 45.00 |
| 1:2 | 26.57 |
| 1:3 | 18.43 |
| 1:4 | 14.04 |
| 1:5 | 11.31 |
| 1:6 | 9.46 |
| 1:7 | 8.13 |
| 1:8 | 7.13 |
| 1:9 | 6.34 |
| 1:10 | 5.71 |
| 1:11 | 5.19 |
| 1:12 | 4.76 |
In case you are wondering, the formula to calculate the angle from a rise:run ratio is this:
arctan(rise/run)
If you want to do this in a spreadsheet, use this:
=DEGREES(ATAN(rise/run))
And here’s the opposite table from a few suitable angles to the corresponding rise:run, if you were wondering:
| Angle (degrees) | Rise:Run |
|---|---|
| 5 | 1:11.43 |
| 6 | 1:9.51 |
| 7 | 1:8.14 |
| 8 | 1:7.12 |
| 9 | 1:6.31 |
| 10 | 1:5.67 |
| 11 | 1:5.14 |
| 12 | 1:4.70 |
| 13 | 1:4.33 |
| 14 | 1:4.01 |
| 15 | 1:3.73 |
| 16 | 1:3.49 |
| 17 | 1:3.27 |
| 18 | 1:3.08 |
| 19 | 1:2.90 |
| 20 | 1:2.75 |
The formula to go from an angle to Rise:Run is this:
Rise = 1
Run = 1/tan(angle)
In case you are wondering what “the correct” angle is - there is no consensus whatsoever. Answers vary greatly depending on who you ask, but everything I have ever seen is between 1:4 (about 14 degrees) and 1:8 (about 7 degrees).